Cryptography - ECC

Elliptic Curve Cryptography (ECC)

Explanation

(1)LOG Problem:

given a, a^x,
we can get x = log_a(a^x)

(2)Elliptive Curve
y² = x³ + ax + b

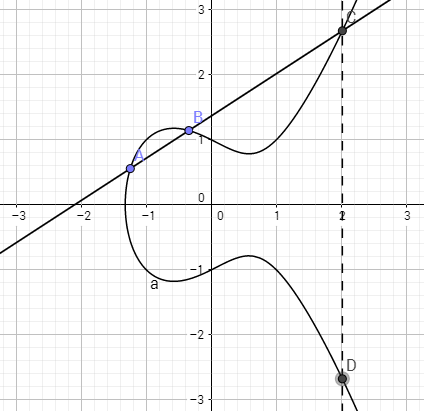
define:

D = A + B     

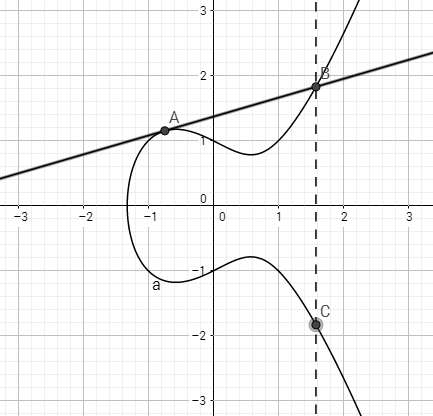
define:

C = A + A     

Let’s further define:

C = A * 2
2 * C = C + C 
3 * C = 2 * C + C  
...
k * C = (k - 1) * C + C  

for any given k and j, it satisfies:
k * (j * C) = (kj) * C= (jk) * P = j * ( k * P )

How to calculate k * C ?

9C (e.g.)  
  
9C = 8C  + C

8C = 4C + 4C 
4C = 2C + 2C    
2C = C + C
it takes 4 mathemetical operations.  
Time Complexity:  
O(logk)  

Question:
Back to (1)LOG problem, given kC, C, can we get k ?
Answer:
Brute-force search, you have to try k one by one.
(3) Elliptic Curve Discrete Logarithm Problem

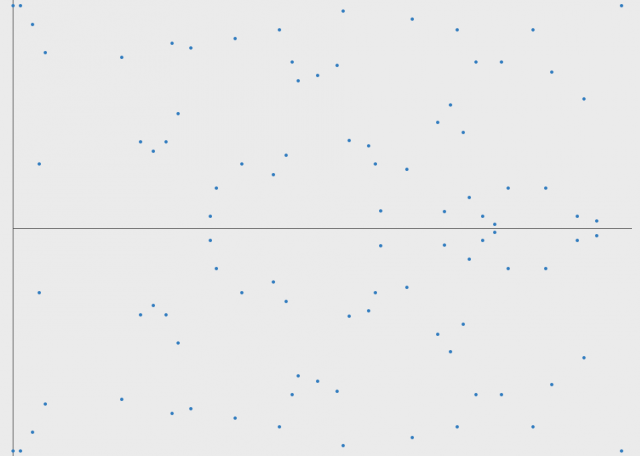
图片参考文献[4]
y² mod 97 = ( x³ - x + 1 ) mod 97

Application - ECDH

How to generate master secret in HTTPs connection?

Key Exchange Based On ECDH (Elliptic Curve Diffie-Hellman)

基于ECC的秘钥交换

服务端确定了密钥协商算法为“EC Diffie-Hellman”，发送给客户端。首先两端都知道了使用的是哪个曲线参数（椭圆曲线E、阶N、基点G）。
premaster secret 计算公式: 用于生成master secret 客户端:
客户端随机生成一个整数c, 计算pubkey_c = c * G

PreMasterSecret：Q = pubkey_s * c = c(s * G)

服务端:
服务端随机生成一个整数s，计算pubkey_s = s * G

PreMasterSecret：Q = pubkey_c * s = s(c * G)

在双方都可能被窃听的环境下，仍能安全交换秘钥。

Bitcoin

Keys

Private Key
Used to generate public key and address.

Randomly generated in 256 binary digits  
 e.g. k =  1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD  (64 hexadeximal digits)  

Public Key

given G(x, y)
K = k * G 
K = (x, y)   
 e.g. x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A  
      y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB  
Public Key =  04xy = 04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB    

Addresses

address = hash_function(public key)    

Wallets

contain cryptographic keys

How To Send And Receive Bitcoin ?

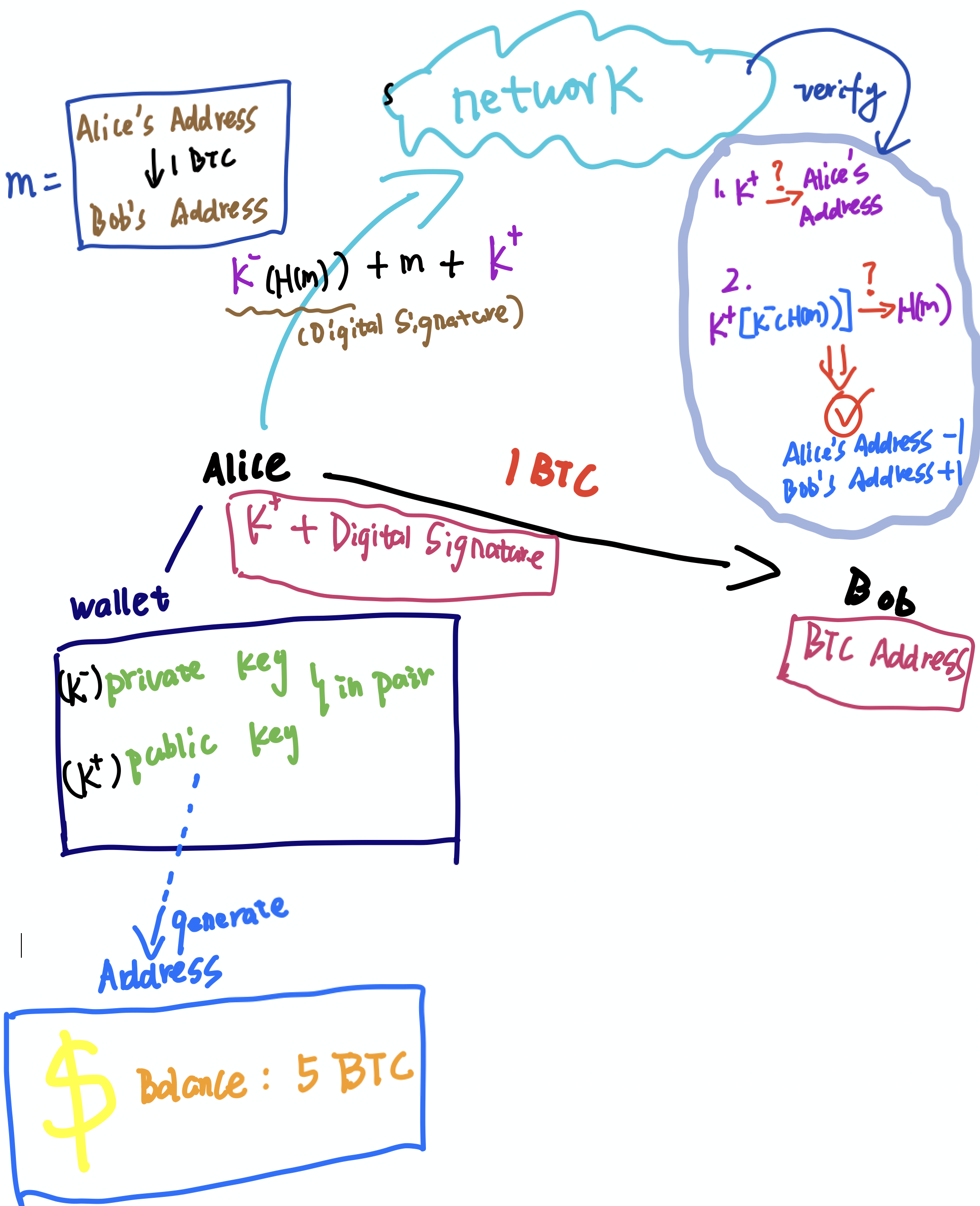
参考

[1^] https://www.bitcoin.com/get-started/how-to-receive-bitcoin/
[2^] https://ririripley.github.io/tech/2021/05/13/about_network_security.html
[3^] http://pangjiuzala.github.io/2016/03/03/Bitcoin%E5%8A%A0%E5%AF%86%E6%8A%80%E6%9C%AF%E4%B9%8B%E6%A4%AD%E5%9C%86%E6%9B%B2%E7%BA%BF%E5%AF%86%E7%A0%81%E5%AD%A6/
[4^] https://blog.csdn.net/qmickecs/article/details/76585303